https://www.zcyphygeodesy.com/en/h-nd-141.html
From the tidal constituent harmonic constant spherical coordinate grid, construct a normalized tidal load spherical harmonic coefficient model and a first-degree tidal load spherical harmonic coefficient model by spherical harmonic analysis.
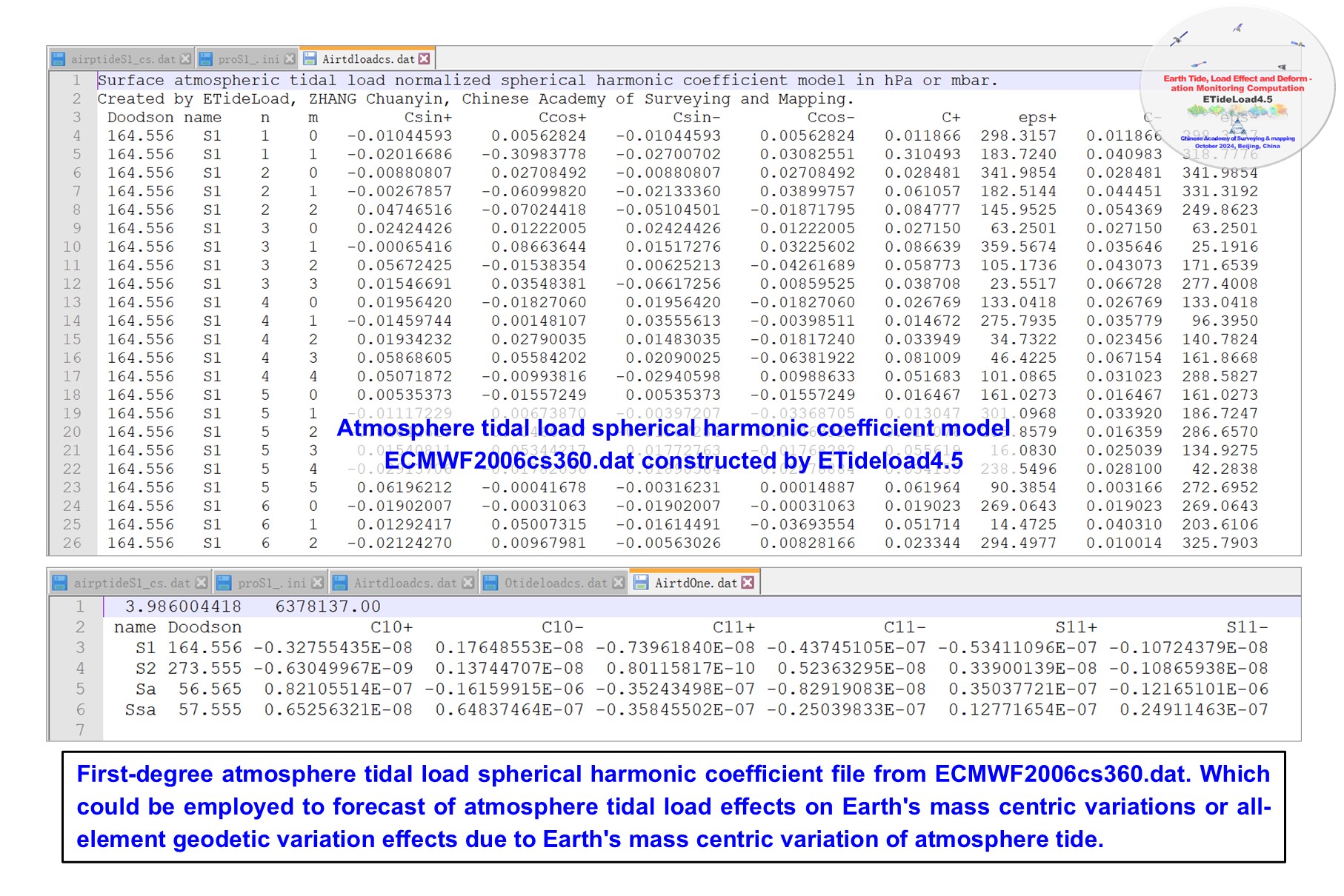
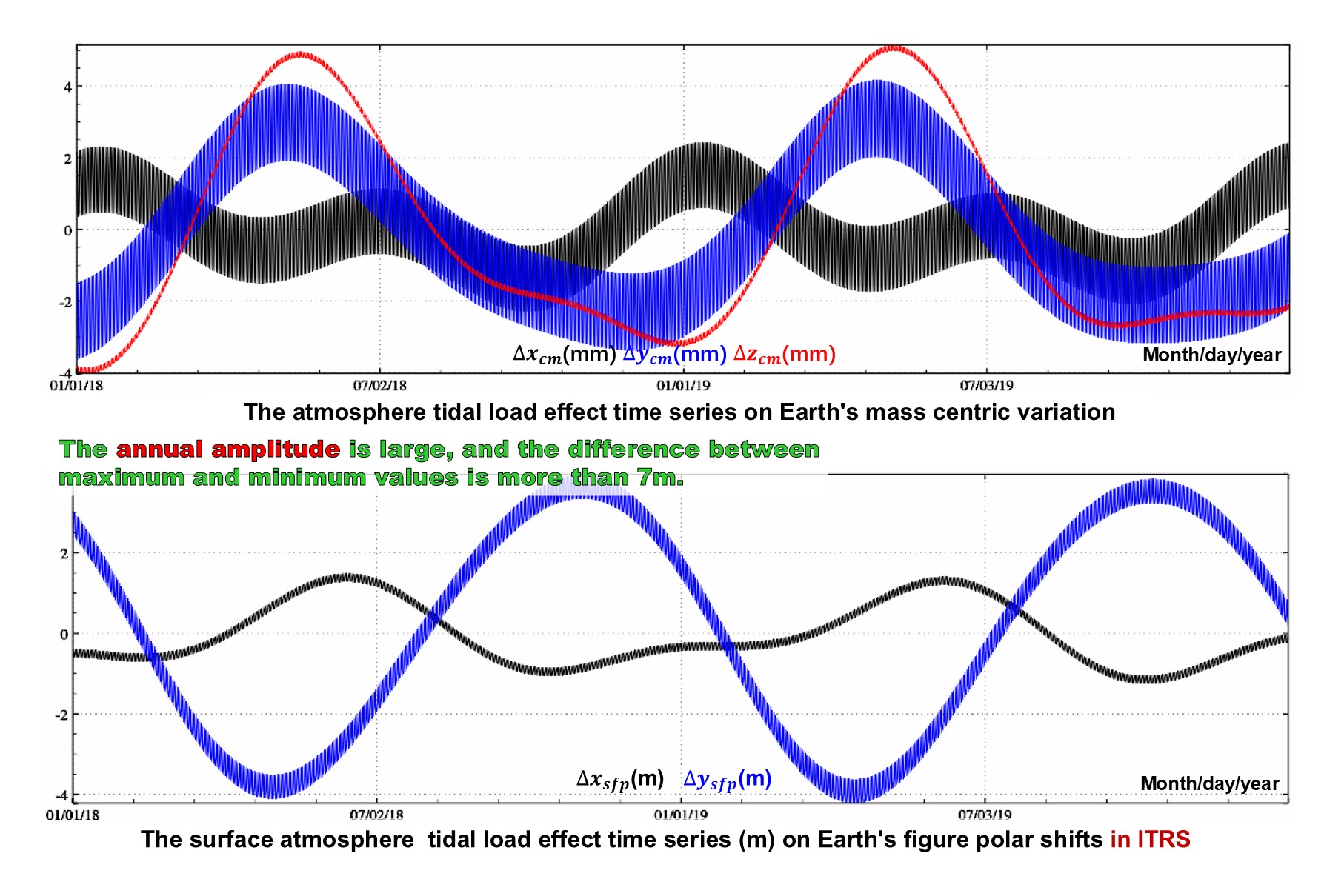
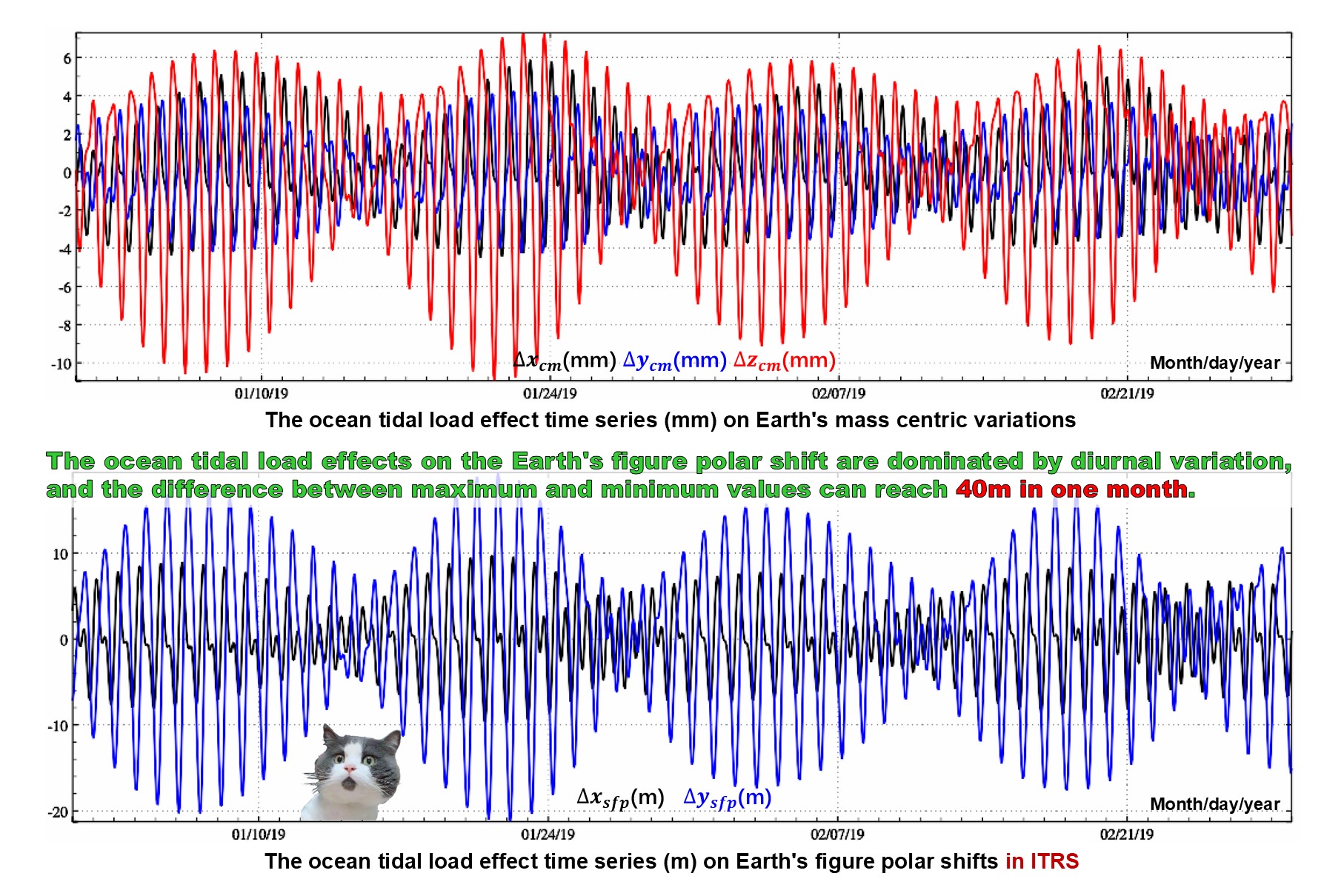
The tidal load spherical harmonic coefficient model format is the same as FES2004 ocean tidal load model in the IERS conventions (2010). Using the model, the tidal load effects on various geodetic variations outside the solid Earth can be computed by the spherical harmonic synthesis.
The first-degree tidal load spherical harmonic coefficient model can be employed to forecast the tidal load effects on Earth's center of mass.
The unit of the tidal constituent harmonic constants is the same as the unit of the tidal load spherical harmonic coefficients. The unit of the surface atmosphere tidal harmonic constants and the atmosphere tidal load spherical harmonic coefficients are hPa or mbar, and the unit of the ocean tidal harmonic constants and the load spherical harmonic coefficients are cm.
The degree number maxn of tidal load spherical harmonic coefficient model is equal to the number of harmonic constant spherical coordinate cell-grids in the latitude direction. For example, the 0.25˚ × 0.25˚ tidal harmonic constant spherical coordinate grid corresponds to maxn=720.

HarmonicanalysisTideLoad.f90
Input parameters: knd - =0 surface atmosphere tide, =1 ocean.
Input parameters: tidefl - = the data file name, in the file include all the tidal constituent harmonic constant spherical coordinate grid file names.
The 7th numerical value of tidal harmonic constant grid file header is the Doodson constant and the 8th attribute is the tidal constituent name. Input parameters: dtmfl - = the land-sea terrain spherical coordinates grid file name. The land-sea terrain grid will be employed for land and sea separation, whose spatial resolution should not be lower than that of the tidal harmonic constant grid. Input parameters: kd, itd - iteration termination condition parameter. The standard deviation of the residual grid value is less than kd of the standard deviation of the original grid value, or the difference of the residual standard deviation of the previous step iteration relative to the current step iteration is less than itd of the standard deviation of the original grid values.
(1) Module for spherical harmonic analysis on all the tidal harmonic constant spherical coordinate grid
Tideharmanalysis(dtmfl,tidefl,knd,dk,itd)
Output files: tidal oad spherical harmonic coefficient model file ***cs.dat, iteration process statistics time series file ***pro.ini and residual grid file ***rnt.dat for each tidal constituent. Here, *** is the tidal constituent name // the Doodson constant.
The module outputs also the normalized tidal load spherical harmonic coefficient model file tdloadharmodel.dat (in FES2004 format) and the first-degree tidal load spherical harmonic coefficient model file tideloadOne.dat into the current directory.
SphHarmExpandFFT(ewh,hd,cilm,2,maxn,nlat,nlon,GRS)
Input parameters: ewh(nlat,nlon) - the tidal constituent harmonic constant grid.
Input parameters: hd(6) - grid specification parameters (minimum and maximum longitude, minimum and maximum geocentric latitude, longitude and geocentric latitude intervals of a cell grid, degree decimal).
Input parameters: GRS(6) - gm,ae,j2,omega,1/f, default value.
Return parameters: cilm(2,maxn+1,maxn+1) - 0~maxn degrees of tidal load spherical harmonic coefficients.
SphHarmExpandFFT(ewh,hd,cilm,2,maxn,nlat,nlon,GRS)
Input parameters: cilm(2,maxn+1,maxn+1) - 0~maxn degrees of tidal load spherical harmonic coefficients.
Return parameters: ewh(nlat,nlon) - the tidal harmonic constant grid.
integralPnm(legI,maxn,hd,lat)
Input parameters: lat - geocentric latitude (degree decimal).
Return parameters: legI(maxn+1,maxn+1) - the numerical integral of associative Legendre function.
BelPnmdt(pnm,maxn,t)
Improved Belikov recursion algorithm for pnm.
LegPn_dt2(pn,dp1,n,t) ! t=cos ψ
PickRecord(line, kln, rec, nn); PickRecstr(line,kln,str,sn); ReimtoHg(xx,x1)
StatGrid(grid,row,col,rst); CGrdPntD2(lon,lat,dtm,nlat,nlon,hd)
Fortran90, 132 Columns fixed format. Fortran compiler. mkl_lapack95_ilp64.lib link library (include fftw3.f)required.
[Algorithmic formula] ETideLoad4.5 User Reference https://www.zcyphygeodesy.com/en/
7.1 Geodetic Data Files in ETideLoad own Format
8.4.1 Construction of tidal load spherical harmonic coefficient model
8.2.3 The normalized associated Legendre functions and thier derivatives
The zip compression package includes the test project in visual studio 2017 - intel fortran integrated environment, DOS executable test file and all input and output data.