-
-
Notifications
You must be signed in to change notification settings - Fork 9
Simulate VAR model
Simone Vazzoler edited this page Apr 13, 2017
·
1 revision
This function can (and should) be used to generate a VAR process of any order.
simulateVAR(N = 100, p = 1, nobs = 250, rho = 0.5, sparsity = 0.05, mu = 0, method = "normal", covariance = "Toeplitz")where the parameters are
-
N: the dimension of the VAR model (defaultN = 100); -
p: the order of the VAR model (defaultp = 1); -
nobs: the number of observation for the series (defaultnobs = 250); -
rho: the intensity of the variance/covariance matrix; -
sparsity: the percentage of non-zero elements in every matrix of the model (defaultsparsity = 0.05); -
mu: an N vector for the mean of the process (defaultmu = 0); -
method: the distribution used to generate the non-zero entries for the matrices of the VAR. Possible values arenormal, bimodal(defaultmethod = "normal"); -
covariance: the type of variance/covariance matrix for the process. Possible values are:block1, block2, Toeplitz, Wishart, diagonal(defaultcovariance = "Toeplitz").
The output of the command
sim <- simulateVAR()is an S3 object (or, if you want, a list), with attr(*, "class") = "var" and attr(*, "type") = "simulation", containing the following elements:
-
A: it is a list ofpsquare matrices of dimensionN; -
series: annobs x Nmatrix containing the simulated series; -
sigma: the variance/covariance matrix of the process; -
noises: thenobs x Nmatrix of the errors.
In the following we will see how to create a (random) VAR model that can be used for testing pourposes.
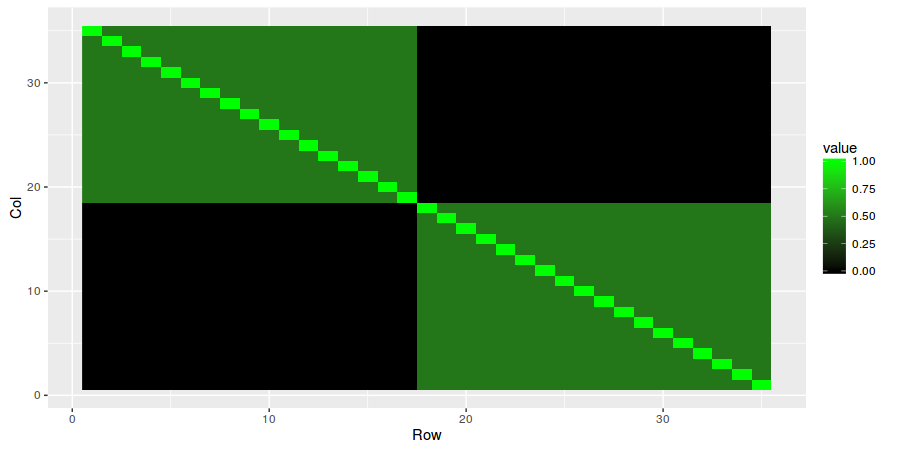
First we initialize the random seed to 0 and then we create a VAR(2) model with dimension N = 35, sparsity = 0.25 and covariance = "block2".
set.seed(0)
sim <- simulateVAR(N = 35, p = 2, sparsity = 0.25, covariance = "block2")To see the results, simply plot the VAR matrices and the variance/covariance matrix.
plotVAR(sim)
plotMatrix(sim$sigma)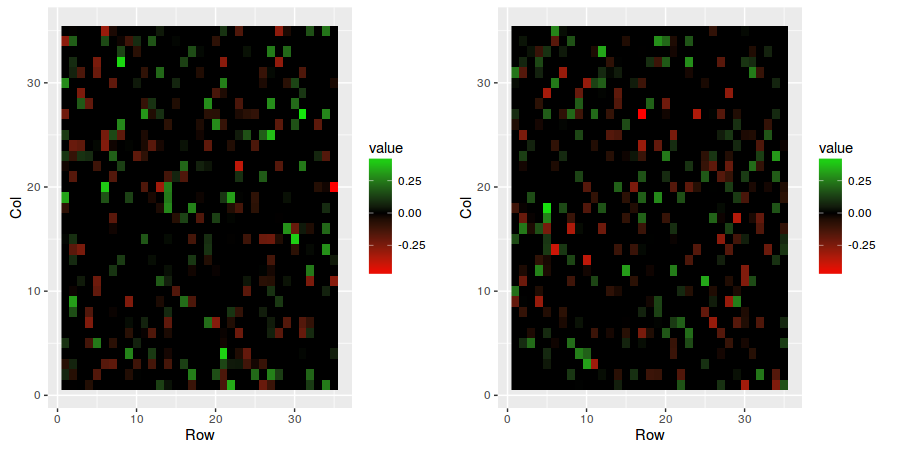
sparsevar package wiki